Nuclear Fission

 

The discovery of neutron by Chadwick in 1932 set up a new field of transmutation reaction by using the neutrons as projectiles. In this line, the work from three groups of scientist: (i) Enrico Fermi in Italy, (ii) F. Joliot Curie and Savitch in France, and (iii) Otto Hahn and Strassman in Germany, paved the way (1934-1938) in discovering the nuclear fission.

In 1936, E. Fermi suggested that the compound nucleus (²³⁶U) formed in the bombardment of slow neutrons on ²³⁵U₉₂ should undergo β^- decay because of a higher neutron to proton ratio in the compound nucleus. This suggestion was tested in laboratory and it showed β^- activity with four different half-lives. Considering four successive β^- decays in the daughter nuclei, there should be four transuranic elements having Z = 93, 94, 95 and 96. The group of J. Curie carried out chemical analysis on the uranium compounds bombarded by the slow neutrons. Astonishingly, they noticed a chemical species having properties close to those of Z = 56-67 far away from Z = 92 in the periodic table. They noticed this surprising observation but did not confirm the observation. Thus the credit of the discovery of nuclear fission slipped away From their hands to the group of Otto Hahn who established barium (Z = 56) as one of the product in the ²³⁵U₉₂ + n reactions. Thus the barium produced showed β^- activity. In the analysis, the production of Krypton (Z = 36) was also proved. Thus, product nuclides were found to be much lighter than the starting nuclide. This is why, it was suggested by Meinter (a former associate of Hahn) and Firsch that the uranium nucleus on being bombarded by a slow neutron, splits into two lighter fragments of comparable size and the process was termed as nuclear fission.

So, we can say that nuclear fission is a nuclear reaction in which the nucleus of an atom splits into two or more smaller nuclei, typically accompanied by the release of a large amount of energy.

²³⁵U₉₂ + ¹n₀ (slow) → ²³⁶U₉₂ → ¹⁴¹Ba₅₆ + ⁹²Kr₃₆ + 3(¹n₀) + energy

Characteristic Features of Nuclear Fission

a) Mass distribution in fission fragments: The compound nucleus formed may undergo fission in a variety of ways. Some possibilities are given below:

 

Thus, the compound nucleus (²³⁶U*) very often undergoes an asymmetric fission in about 30 routes. The mass number of the lighter fission product lies in the range 85 to 104, while the heavier fragment covers the range, 130 to 149. The most probable fission path involves the fragments with mass numbers around 95 to 139. The distribution of mass number can be represented in the fission yield curve known as Bohr yield curve.

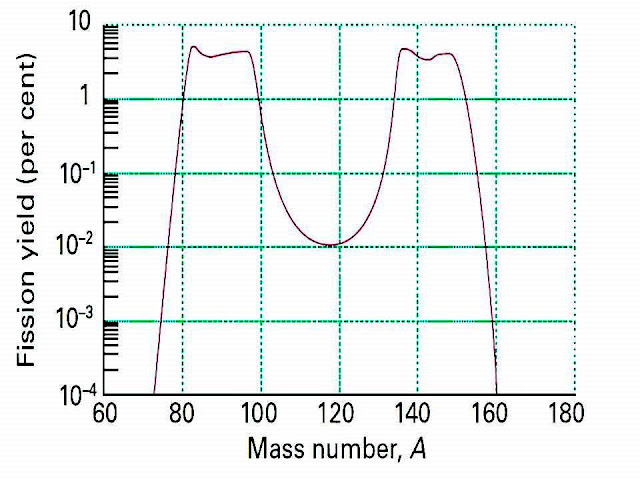Fission yield curve (known as Bohr yield curve)

The symmetric fission producing the fragments with mass number -117 is a rare possibility and it is evident. However, it has been proved that with the increase of energy of the projectile neutron affecting the fission, the probability of symmetric fission increases. It is experimentally verified in 239Pu.

b) Energy distribution in fission fragments: The mass distribution pattern is intimately related with the energy distribution pattern among the fission products. If the compound nucleus undergoing fission is assumed to be at rest, and the energies shared by the emitted neutrons are neglected, then according to the law of conservation of momentum, it gives,

M₁u₁ = M₂u₂

Or, u₁/u₂ = M₂/M₁

Where M₁ and M₂ denote masses of the two fragments, and u₁ and u₂ represent their corresponding velocities. Therefore, for kinetic energies

E₁/E₂ = [½ M₁u₁²]/[ ½ M₂u₂²] = M₂/M₁ (as M₁u₁ = M₂u₂)

Thus, the masses and kinetic energies of the fragments are inversely related. The distribution of kinetic energy among the fission products can be measured by using an ionisation chamber.

c) Emission of projectiles: The projectiles affecting the nuclear fission are emitted (2-3 per fission) in the process. Thus, the ejectiles under a suitable condition can be reutilized as projectiles to make the process self-sustained.

Here, it is worth mentioning that all the neutrons are not emitted at one instant. More than 99% are emitted almost instantaneously in a time of the order of 10^-14 s. These neutrons are called prompt neutrons. The neutrons (1%) which are emitted in late from the fission products are called delayed neutrons.

Prompt neutrons are released within 10^-14 s from the neutron-rich fragments of fission products. Thus the fission of ²³⁵U by a thermal neutron can be represented as:

²³⁵U₉₂ + ¹n₀ → (²³⁶U₉₂*) → ¹⁴⁶La₅₇ + ⁸⁷Br₃₅ + 3(¹n₀) (prompt neutrons)

Here, ⁸⁷Br is a β^- emitter and it decays with a half-life of 55.5 s to ⁸⁷Kr which is sufficient energy to eject a neutron immediately to produce the stable nuclide ⁸⁶Kr, i.e.

⁸⁷Br → ⁸⁷Kr* + β- → ⁸⁶Kr + n (delayed neutron)

Here, the neutron emission rate is determined by the slow step (t_1/2 = 55.5 s). Such neutrons, emitted after a measurable time period of the fission are described as delayed neutrons which play an important role in controlling the nuclear fission in nuclear reactors. The delayed neutrons are of low energy while the prompt neutrons are of high energy.

d) β^- Activity in the fission products: In the products fragments, the neutron to proton ratio lies far above their corresponding stability region. The starting nuclide (Z = 92) requires a relatively higher neutron to proton ratio for its stability and this high ratio on being transmitted to the fission products of much lower atomic number makes them unstable with respect to β^- activity. The process goes on until the stable nuclei are formed. Thus in a particular fission reaction, two different series of isobaric nuclides with the mass number A₁ and A₂ (where the initial fragments are characterized with the mass number A₁ and A₂) are obtained. The β^- activities of some fission products are shown below.

e) Energy (Q) release in fission: The energy released per fission is ≈ 200 MeV which is much greater than that released in any ordinary nuclear reaction. Due to the ejection of the projectiles, once the process is started, it can process in a chain reaction to release an enormous amount of energy in a moment. The calculation of energy release in the process can be done in two ways as discussed below.

i) Mass defect method:

For this purpose, let us consider one of the most probable fission reactions, i.e.

²³⁵U₉₂ + ¹n₀ → ⁹⁸Mo₄₂ + ¹³⁶Xe₅₄ + 2(¹n₀) + 4 (⁰e_-1) + 4 (⁰ν₀)

Here, mass loss Δm ≈ [ m(²³⁵U) + m(¹n)] – [m(⁹⁸Mo) + m(¹³⁶Xe) + 2m(¹n)]

= (235.044 + 1.0086) – (97.906 + 135.907 + 2×1.0086)

= 0.2224 amu or (0.2224×931) MeV = 207 MeV

In calculating Δm, the mass of the emitted electrons has been neglected.

ii) Nuclear binding energy (NBE) method:

For the nuclear binding energy curves, it is evident that for the fissionable nuclides (A ≈ 235 – 240), the binding energy per nucleon lies in the range ~ 7.5 MeV while the fission products stand on the curve where B ~ 8.5 MeV. Thus in moving from the position of the fissionable nuclide to that of the fission products, ~1 (= 8.5-7.5) MeV energy is released per nucleon. Thus in each fission, ~235 × 1 = 235 MeV energy is released (neglecting the neutrons emitted as ejectiles).

Reference

1) Concise inorganic chemistry by J. D. Lee.

2) Inorganic Chemistry by James E. Huheey, Ellen A Keither, Richard L. Keither, Okhil K. Medhi.