The Photoelectric Effect

Characteristics of Photoelectric Effect

When a beam of light (in some cases visible light) is incident on a metal plate preferably of alkali and alkaline earth metals, some electrons are emitted. An experiment design is shown here when a beam of light is getting incident on the metal surface (P) in an evacuated tube, the emitted electrons from the metal plate are attracted to the positively charged plate (Q). Thus a current flow through the circuit and it can be detected by the galvanometer (G). This photoelectricity follows the following characteristic features supported by the experimental facts.

a) Dependence of photoelectric current on the intensity of incident light: The total photoelectric current (i.e. the total number of electrons emitted from a given surface) is proportional to the intensity of the incident beam of a particular frequency. Intensity of a beam of a particular frequency is measured by the number of photons getting incident per unit area of the surface per second. Thus it indicates, the greater the number of incident photons of a particular frequency, the greater is the number of emitted electrons and hence the more current is produced.

b) Threshold frequency of the incident light to initiate the photoelectric effect: For a particular metal surface, the incident beam should have a minimum frequency below which there will be no emission of electrons. This minimum frequency required to start the phenomenon is called the threshold frequency of that particular metal. If the threshold frequency is not attended, whatever may intensity of the incident beam there will be no photoelectric current.

c) Dependence of energy of the emitted electrons on the frequency of incident beam: The maximum velocity, or the maximum kinetic energy of the emitted electrons for a particular metal plate is completely independent of the intensity of the incident beam, but the maximum energy of the electrons is dependent on the frequency of the incident beam. Thus the maximum energy of the electron is only dependent on the frequency of the incident beam and nature of the metal.

The above facts can be illustrated experimentally. In the figure if the plate (Q) is made negative with respect to metal surface (p) then the emitted electrons will experience a retarding potential to reach the collector plate (Q). The electrons which will have only sufficient kinetic energy to overcome the retarding potential will only be able to reach the plate. Thus, if the retarding potential is increased gradually for a particular incident beam of a certain frequency, then at a certain potential it will be found that no emitted electron will be able to reach the collector plate. This minimum required retarding potential to stop the photoelectric current is called the stopping potential (V_s).

½ mu_max² = eV_s or u_max = √(2eV_s/m)

Here it is noteworthy that all the electrons emitted are not having the same velocity. The electrons emitted just from the surface will have the maximum energy while the electrons coming from the bulk will have the lower energy. Thus the energy of the electrons may vary, but the maximum energy which can be associated with the emitted electrons is fixed for a certain frequency of the beam incident on a particular metal surface. Thus, stopping potential is found to increase linearly with the increase of frequency of the beam while it is independent of the intensity of the beam.

Now, the potential of the collector plate is moved towards the positive direction with respect to plate (P) and the current goes to increase. But after certain positive value of the potential on Q, there will be no further increase of current. This is called saturation current. It means that all the liberated electrons having energy, minimum (i.e. u_min) to maximum (i.e. u_max) have been able to reach the collector plate.

Einstein’s Theory of Photoelectric Effect

According to Einstein's theory, when a photon strikes an electron, either the whole energy of the photon or no energy of the photon will be transferred to the electron. Thus it follows the principle, all or none. If a photon gets incident on the metal surface and the energy transfer process occurs then a proportion of the energy will be used to make the electron free from the binding forces of the metal and the residual energy will be utilized to import the kinetic energy to the released or free electron.

If the target electron lies below the surface, it will require some additional amount of energy to reach the surface, but if the target electron originates on the surface, it will not require this additional energy. Thus the energy of the incident photon will be utilized in three different successive steps:

(i) bringing the target electron to the surface from the binding forces within the metal,

(ii) releasing the electron from the surface, and

(iii) imparting the kinetic energy to the released electron of zero velocity on the surface.

This is why, for a particular type of photons of hν, the electron which originates on the surface will have maximum kinetic energy because it does not require any additional energy as required by the bulk electron. Under such circumstances, the electron on the surface will required the minimum amount of energy (ω) to overcome the binding forces to get released. This minimum energy, ω represents the work function of the metal and it is expressed in terms of threshold frequency (ν_o) as ω = hν_o. It indicates that the energy of the incident photon is less than ω or hν_o, there will be no emission of photoelectron.

In view of the above fact, for the incident photon of hν, according to the principle of conservation of energy, it can be written as follows:

½ mu_max² + ω = hν

½ mu_max² = hν - hν_o

eV_s = h(ν – ν_o)

This is the Einstein's equation. The above equation can explain all the observations which did not get any support from the idea of classical electromagnetic theory. It implies the following conclusions:

Concept of threshold frequency or work function: If the frequency of the incident photon is less than the threshold frequency ν_o (in terms of energy, hv < work function, ω), there will be no photoelectric emission, regardless of the intensity (i.e. the number of photons getting incident on the metal surface per unit area per second).

Relationship between stopping potential and frequency of the incident beam: The maximum kinetic energy and consequently the stopping voltage (V_s) are independent of the intensity of the incident photon but linear relationship with the frequency of the incident photon. This aspect was verified experimentally by Millikan. According to the Einstein's equation we have:

V_s = hν/e – ν_o/e

Thus the plot of V_s against ν gives straight line whose slope is given by h/e and the magnitude of the intercept is given by hν_o/e. From the slope, h can be obtained from the known value of charge of the electron. Millikan determined the value of Planck constant in this method and it was in good agreement with the result obtained from other sources this verification definitely gives a sound support to the validity of Einstein's equation.

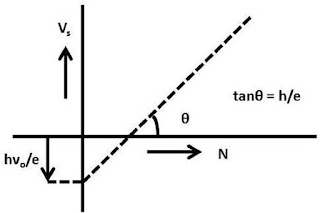Variation of stopping voltage for the emitted photoelectrons with the frequency of the incident radiation

Work function and ionization potential:

The electrons in a metal are having some potential energy. The potential energy of an electron for a particular metal depends on its position. The electrons at the outermost shell of the atoms deciding at the surface are having the minimum binding energy. On the other hand, for the same type of electrons within the bulk, the binding energy is higher. This is why; the most loosely bound electrons (i.e. At the outermost shell) of the atoms at the surface require the minimum amount of energy to get released from the binding forces. The minimum required energy is called the work function of the metal. In the case of ionization potential, it gives the required minimum amount of energy to release the most loosely bound electron from the metal atom in isolated and gaseous condition. Thus both the process deal with the required minimum amount of energy to knockout the most loosely bound electron. But in the case of photoelectric effect, the metal atom is in the solid state at the exposed surface while in the case of ionization potential, the metal atom is in gaseous or isolated condition.

Metal	λo (nm) (threshold)	Work function (in eV)	Ionisation (1st) potential (eV)
Na	500	2.50	5.12
K	550	2.26	4.32
Cs	660	1.87	3.88
Cu	290	4.30	7.70
Ag	261	4.73	7.54
Zn	359	3.44	9.37
Fe	262	4.71	7.83
W	261	4.73
Pt	196.2	6.30

In this table a comparison between the ionization potential (first IP) and work function of some metals are given. It is evidence that the more ionization potential, the more is the work function. This is why; alkali metals are very often used in photoelectric cells. The magnitude of work function is always lower compared to its corresponding ionization potential. It indicates that for releasing an electron from an atom present in the aggregate form, it requires less energy compared to the process of releasing the electron present in an atom in isolated and gaseous condition.

Reference

1) Concise inorganic chemistry by J. D. Lee.

2) Inorganic Chemistry by James E. Huheey, Ellen A Keither, Richard L. Keither, Okhil K. Medhi.